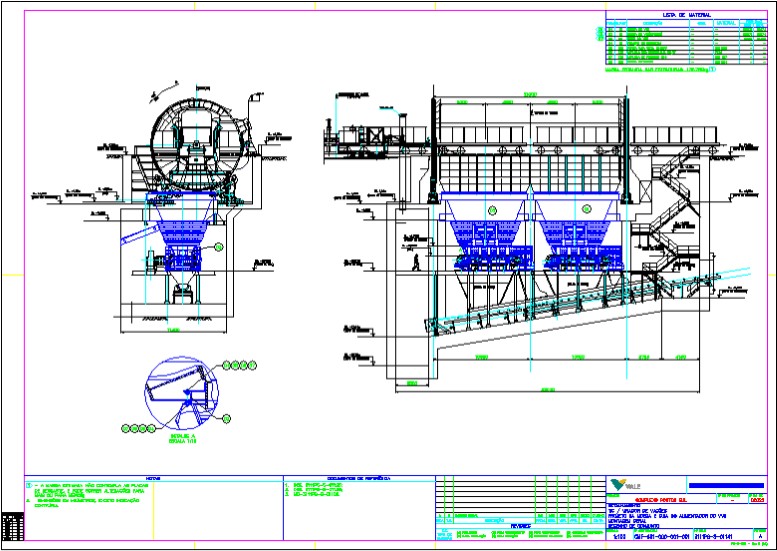
Análise Estrutural (Elementos Finitos)
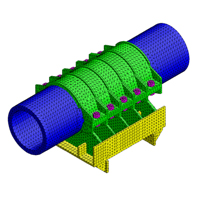
O Método dos Elementos Finitos (FEM) consiste em diferentes métodos numéricos que aproximam a solução de problemas de valor de fronteira descritos tanto por equações diferenciais ordinárias qanto por equações diferenciais parciais através da subdivisão da geometria do problema em elementos menores, chamados elementos finitos, nos quais a aproximação da solução exata pode ser obtida por interpolação de uma solução aproximada. Com este tipo de método são determinados, por exemplo, tensões, deslocamentos,deformações, frequências naturais de vibração, modo de flambagem, etc... Os tipos de análises já executados pelas CEMEF são:
- Análises estruturais - Estáticas, dinâmicas, fadiga, otimização estrutural (lineares e não-lineares).
- Análises térmicas - Estacionárias e transientes, lineares e não-lineares.
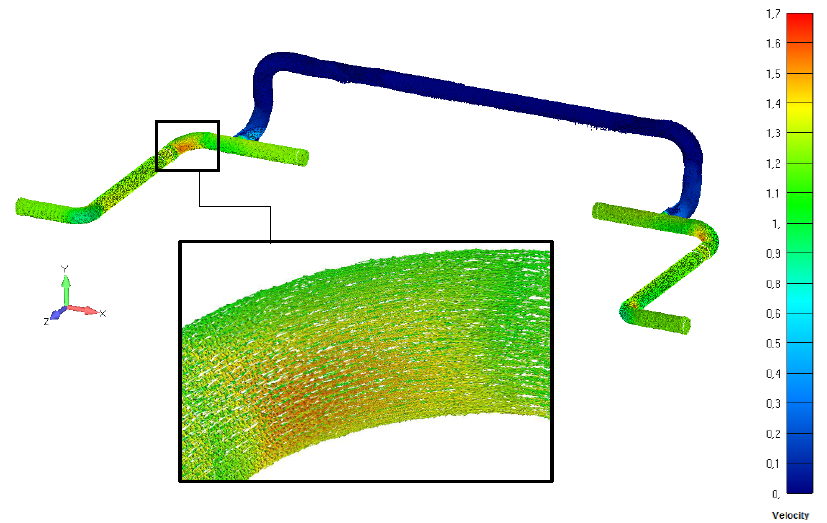
- Dinâmica de fluidos computacional - CFD, problemas de escoamento de fluidos.
- Estática linear - Verificação de deslocamentos e tensões.
- Flambagem linear - Verificação de estabilidade.
- Estática não-linear - Problemas de grandes deslocamentos, conformação mecânica envolvendo plasticidade e flambagem.
- Térmica estacionária - Determinação da distribuição de temperaturas considerando-se condução, convecção e radiação.
- Térmica transiente - Variação temporal da distribuição térmica.
- Modal - Determinação de modos e freqüências naturais de vibração), com e sem efeitos de enrijecimento / amolecimento.
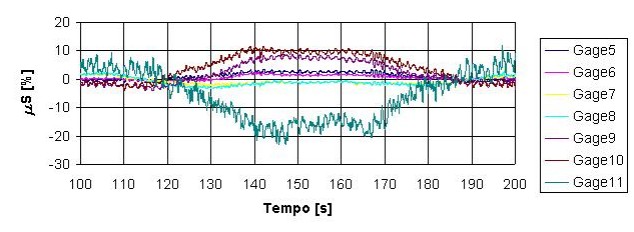
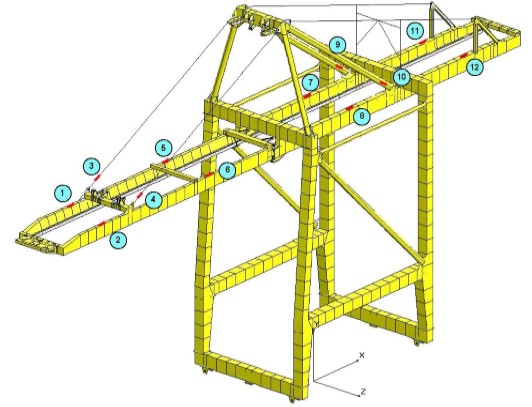
- Dinâmica de resposta no tempo - Cargas ou excitações de base variáveis e choques mecânicos, também utilizadas em simulações de testes dinâmicos.
- Dinâmica de resposta harmônica - Cargas ou excitações de base senoidais / cossenoidais.
- Dinâmica de resposta aleatória - Cargas ou excitações de base randômicas.
- Dinâmica de resposta espectral - Utilizada principalmente em análises envolvendo terremotos (cargas sísmicas).
- Dinâmica não-linear - Cargas variáveis no tempo envolvendo problemas de contato.
- Fadiga - Cargas variáveis no domínio do tempo, determinação da falha.
- Otimização estrutural - Permite otimização em termos de forma e tamanho.